Spostamento verso il rosso cosmologico

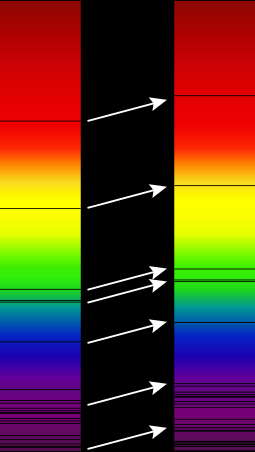
Lo spostamento verso il rosso cosmologico (detto anche redshift cosmologico) è lo spostamento relativo in frequenza di un'onda elettromagnetica dovuto all'espansione dell'universo. Inizialmente lo spostamento verso il rosso veniva attribuito all'effetto Doppler, tramite la relazione

${\displaystyle z\approx {\frac {v_{r}}{c}}}$

ma l'osservazione sperimentale di alcuni quasar caratterizzati da uno spostamento verso il rosso compreso tra 5 e 6 ha smentito tale ipotesi. L'approssimazione del redshift come effetto Doppler è valida solo se ${\displaystyle z\ll 1}$. Il redshift cosmologico si spiega ipotizzando che le lunghezze d'onda varino allo stesso modo delle distanze per effetto dell'espansione dell'universo. Ciò è verificato dal teorema del redshift.

Ipotesi

Supponiamo che l'universo si stia espandendo, e che tutte le distanze varino secondo un fattore di scala ${\displaystyle a(t)}$ per cui possiamo ipotizzare

${\displaystyle D=a(t)r}$

dove ${\displaystyle r}$ è la coordinata comovente, ovvero un tipo di coordinata che segue punto per punto l'espansione dell'universo.

Teorema del redshift

Il teorema del redshift afferma che la lunghezza d'onda ${\displaystyle \lambda }$ è proporzionale al fattore di scala dell'universo.

Consideriamo la metrica di Friedmann-Lemaître-Robertson-Walker

${\displaystyle ds^{2}=c^{2}dt^{2}-a^{2}(t)\left[{\frac {dr^{2}}{1-kr^{2}}} r^{2}(d\theta ^{2} \sin ^{2}d\phi ^{2})\right]}$

dove ${\displaystyle k}$ è il parametro che identifica i tre diversi modelli di Friedman. Ora supponiamo di osservare un quasar posto ad una distanza comovente ${\displaystyle r_{1}}$ dalla terra (che assumiamo posta nel punto ${\displaystyle r=0}$) e sotto i due angoli costanti ${\displaystyle \theta }$ e ${\displaystyle \varphi }$. In tali condizioni la metrica si riduce a

${\displaystyle ds^{2}=c^{2}dt^{2}-a^{2}(t){\frac {dr^{2}}{1-kr^{2}}}}$

ora considerando che stiamo osservando un'onda elettromagnetica dobbiamo porre ${\displaystyle ds^{2}=0}$ ottenendo

${\displaystyle {\frac {dt}{a(t)}}=-{\frac {dr}{\sqrt {1-kr^{2}}}}\qquad \quad (1)}$

(si osservi che c è stata posta uguale ad 1, ed il segno meno è dovuto al fatto che, al crescere di t, r diminuisce, in quanto l'onda elettromagnetica si avvicina alla terra con il passare del tempo).

Ci conviene ora considerare due creste consecutive dell'onda elettromagnetica: la prima emessa ad un tempo ${\displaystyle t_{1}}$ e ricevuta ad un tempo ${\displaystyle t_{0}}$, e la seconda emessa ad un tempo ${\displaystyle t_{1} \delta t_{1}}$ e ricevuta ad un tempo ${\displaystyle t_{0} \delta t_{0}}$.

Integrando la (1) per le due creste separatamente otteniamo

${\displaystyle \int _{t_{1}}^{t_{0}}{\frac {dt}{a(t)}}=\int _{0}^{r_{1}}{\frac {dr}{\sqrt {1-kr^{2}}}}\equiv F(r_{1})}$

${\displaystyle \int _{t_{1} \delta t_{1}}^{t_{0} \delta t_{0}}{\frac {dt}{a(t)}}=\int _{0}^{r_{1}}{\frac {dr}{\sqrt {1-kr^{2}}}}\equiv F(r_{1})}$

Dal momento che gli integrali al secondo membro sono uguali possiamo eguagliare gli integrali al primo membro delle due espressioni:

${\displaystyle \int _{t_{1}}^{t_{0}}{\frac {dt}{a(t)}}=\int _{t_{1} \delta t_{1}}^{t_{0} \delta t_{0}}{\frac {dt}{a(t)}}}$

${\displaystyle \int _{t_{1}}^{t_{0}}{\frac {dt}{a(t)}}=\int _{t_{1}}^{t_{0}}{\frac {dt}{a(t)}} \int _{t_{0}}^{t_{0} \delta t_{0}}{\frac {dt}{a(t)}}-\int _{t_{1}}^{t_{1} \delta t_{1}}{\frac {dt}{a(t)}}}$

${\displaystyle \int _{t_{0}}^{t_{0} \delta t_{0}}{\frac {dt}{a(t)}}=\int _{t_{1}}^{t_{1} \delta t_{1}}{\frac {dt}{a(t)}}}$

A questo punto consideriamo il fatto che la variazione del fattore di scala è molto lenta nel tempo ${\displaystyle ({\dot {a}}/a\ll 1)}$. Possiamo considerare il fattore di scala costante sia durante l'emissione delle due creste, sia durante la ricezione, e ottenere

${\displaystyle {\frac {\delta t_{1}}{a(t_{1})}}={\frac {\delta t_{0}}{a(t_{0})}}}$

e quindi

${\displaystyle {\frac {\delta t_{0}}{\delta t_{1}}}={\frac {a(t_{0})}{a(t_{1})}}}$

moltiplicando e dividendo il primo membro per ${\displaystyle c}$ si ottiene

${\displaystyle {\frac {\lambda (t_{0})}{\lambda (t_{1})}}={\frac {a(t_{0})}{a(t_{1})}}\qquad \Rightarrow \qquad \lambda (t)=\lambda (t_{0}){\frac {a(t)}{a(t_{0})}}}$

il che è esattamente quello che intendevamo dimostrare.

Il redshift cosmologico

Se consideriamo, quindi, la definizione di "spostamento verso il rosso" abbiamo:

${\displaystyle z={\frac {\lambda _{o}-\lambda _{e}}{\lambda _{e}}}}$

dunque, nel caso dello spostamento verso il rosso cosmologico si ottiene

${\displaystyle z(t)={\frac {a(t_{0})}{a(t)}}-1}$

Note

Voci correlate

• Spostamento verso il rosso
• Spostamento verso il rosso gravitazionale
• Coordinate comoventi
• Metrica di Friedmann-Lemaître-Robertson-Walker
• Universo in accelerazione